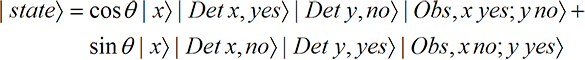Applications of
Quantum Mechanics
Implications of
Quantum Mechanics
32. Light, Photons and Polarization.
Summary
The polarization states of photons are explained. Polarization experiments on light are described.
A photon is the name given to a ‘piece’ of light. In this treatment, where it is justifiably assumed there are no particles (see
No Evidence for Particles), it refers to a wave function with mass 0, spin 1, and charge 0. Each photon (wave function) travels at the speed of light. If it has wavelength
, its energy is
hc/
and its momentum is
h/
where
c is the speed of light and
h is Planck’s constant.
Each photon has two possible states of
polarization, which is analogous to spin or angular momentum (See
Spin and the Stern-Gerlach Experiment). This can be visualized in the following way: A photon can be thought of (at least classically) as consisting of oscillating electric and magnetic fields. If a photon is traveling in the z direction, its electric field can either oscillate in the x direction, so the photon is represented by
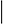 x
x
, or its electric field can be oscillating in the y direction, so it is represented by
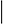 y
y
. These are the two states of polarization.
It can also be polarized so its electric field oscillates in any direction, say at an angle
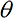
to the x axis. In that case, the photon state can be represented as a (linear)
combination of the
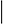 x
x
and
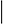 y
y
polarizations,
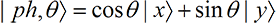

(32-1)
There are certain materials (such as Polaroid) that act as filters in that they let through only that part of the photon polarized in a certain direction. Schematically, in terms of the wave function, if we have a polarizer
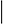 P,x
P,x 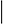
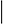
that lets through only
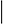 x
x
photons, then the
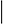 y
y
part is blocked, so
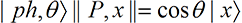

(32-2)
What this translates into experimentally is the following: Suppose we have a beam of light that contains N photons in state (32-1) crossing a given plane per sec., each moving at the speed of light. Then a 100% efficient detector put in the beam will record N ‘hits’ per second. But if we put an
x polarizer in the beam, as is done schematically in (32-2), the detector will record only
N cos2 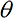
hits per second. And if we put in a
y polarizer, the detector will record only
N sin2 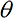
hits per second. (This is in agreement with the
|ai|2 probability law of principle [
P10] in
The Probability Law.
Thus the polarization state of Eq. (32-1) acts
as if it were composed of both a photon polarized in the
x direction
and a photon polarized in the
y direction. But if we measure, we find an
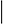 x
x
photon on a fraction
cos2 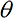
of the measurements and a
 y
y
photon on a fraction
sin2 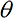
of the measurements, but we never find both an
 x
x
photon and a
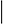 y
y
photon on a single run! Not so easy to understand!
There are crystals that can separate the photon into its
x and
y polarization parts, so that the
x polarized part travels on one path and the
y polarized part travels on another path. One can put a detector in each path, and one can have an observer that looks at each detector. If we send a single photon, in state (32-1), through this apparatus, the wave function of the two detectors plus the observer is still a sum of just two terms:
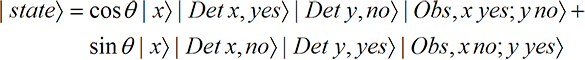

(32-3)
But now the whole ‘universe,’ photon, detectors and observer, has split into two states. In particular, if you are the observer, there are two states of you! On a fraction
cos2 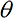
of the runs, the “
x, yes;
y, no” version will correspond to your perceptions; and on a fraction
sin2 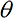
of the runs the “
x, no;
y, yes” version will correspond to your perceptions. On a given run, quantum mechanics does not say which version will correspond to your perceptions. So this experiment and the state of Eq. (32-3) give another example of quantum mechanics presenting us with more than one version of reality—one version of you perceiving polarization
x and, at the same time, another version of you perceiving polarization
y.