We wish to indicate here that quantum mechanics does not conflict with our perception of a seemingly classical world. The main ideas used are that only versions of the observer perceive (Schrödinger’s Cat, principle [P2]) and that the versions of reality, including the versions of the observers, are in isolated, non-communicating universes (Separate Universes in Quantum Mechanics).

To illustrate the principles, we consider an experiment on an atomic system with K states, k. There is an apparatus with state vector A and an observer with state vector O. After the experiment is done, the state is
Perception of a single version. Before the experiment starts, we tell the observer to write down ‘1, classical’ if they see just one version of reality, and ‘other’ if they perceive anything else (such as a ‘double exposure’). We see from Eq. (9A-1) that each version will write down ‘1, classical;’
“Other” is never written. Even if we switch bases, so that each version of the observer is a linear combination of the O_k , ‘other’ will never be written because O_k in the linear combination is still just O_k (1,classical). And since ‘other’ is never written, it must never be perceived. Thus, since only versions of the observer perceive, and all perceptions by versions of the observer are of single versions of reality, we have

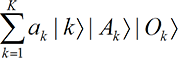
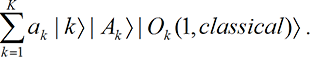
[P6] Basic quantum mechanics prohibits perception of more than one version of reality.

Observers must agree. Next we consider principle [P7], on the agreement of observers. We ask two observers to write down their perceptions and then ask the second observer to look at the first observer’s result and write “agree” or “disagree.” Because the interactions are local and separable, a cause in the past can never produce a classically inconsistent effect in the future within a version. This general principle implies that the state vector is

Thus “disagree” is never written, so

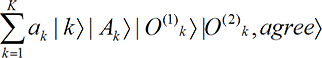
[P7] Quantum mechanics implies that two observers can never disagree on what they perceive.

Successive observations are consistent. We now consider principle [P8]. We start from state (9A-1) and have the observer look twice at the dial. Then we have state
Thus we see we never have O (k, j) so that an observer never has conflicting memories:

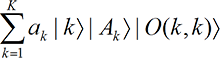
[P8] If two observations of a single result are made successively, quantum mechanics implies the same consistency of results as one obtains in a classical universe.

The same argument would apply if one did multiple experiments; results are always consistent within a version, and versions of the observer cannot ‘see’ from one isolated universe to another.

Finally, we consider principle [P8], in the technical case, on the consistency of successive measurements. As an example, we might have a spin Stern-Gerlach experiment that yields two different possible trajectories for the particles exiting the apparatus. We then put a second Stern-Gerlach experiment in each exit beam to re-measure the z-component of spin. We will find that we get consistent results, both experimentally and quantum mechanically.

To actually write out the states to show this is a notational nightmare, so we will talk it through. We suppose there is a device, M, that splits the beam of incoming particles into N different trajectories, and on each trajectory, there is a readout, R, that says no (no detection) or yes (detection). Then on each of the N possible trajectories, we put a similar device, M plus a similar readout. We designate the state of the apparatus before the experiment by a 0 subscript. Then for any of the N+1 sets of apparatus, we have

and hence for the special case

where there is no sum in Eq. (9A-6).
Now we do the compound experiment. After the first apparatus, there will be N versions of reality. In version k, there will be the particle state, k, plus a readout that says k yes, all others no. Now when the particle state k hits the second apparatus, because of Eq. (9A-6), that apparatus will also register k yes, all others no. Thus the second measurement must agree with the first, even if there is no collapse or no actual particle in a certain state. And so we have

If one measures the same property twice in a row, quantum mechanics implies one will get the same result.

In summary, the perceptions of ‘the observer’ in quantum mechanics will never disagree with what is expected classically. (So the only problem with quantum mechanics is that we don’t know which version of reality will pop up.)

Measurement Theory The principles of Quantum Mechanics and Classical Perception constitute much of the content of what is called measurement theory. Only in measurement theory, they are taken as axioms, needed to make sense of measurements in quantum mechanics, rather than as principles deduced from quantum mechanics itself. These derived principles show that in all circumstances, quantum mechanics itself implies a ‘classical’ consistency of perceptual results—‘measurements’—even though no classical (that is, single-version-of-reality, effect-follows-from-cause) reality was assumed.
We note that, there is a principle on the perception of eigenvalues, which should have been derived before principle [P8]. It is derived as principle [P8A] in section 14B.

Superselection rule. Preferred basis problem. The principles of Quantum Mechanics and Classical Perception also imply it is appropriate to apply a superselection rule to the various versions of reality. Linear combinations of, say, the various states of the observer are not prohibited, but (as in the case where one has one universe with charge 2e and another with charge 3e) when there is no interaction between different solutions of the Schrödinger equation, nothing—no new physical insight—is gained by considering linear combinations of the states.
Thus the preferred basis problem, in which linear combinations of versions of the observer are considered, seems to be a red herring (see also the derivation of principle [P6] and Measurement Theory). No version of the observer will ever perceive anything besides a single version of reality.
More specifically, if the versions of the observer write down what they perceive, no version of the observer will ever write down that she perceives anything other than a single (classical) version of reality, no matter what basis one uses. Suppose, for example that we have two final states, 1 and 2. Then one might try a basis where ‘the observer’ has states

But there is still no term where the observer writes down that she perceives both states 1 and 2. And the two parts of are unaware of each other because they are in different, non-communicating universes. That is, as in any case where one has a superselection rule, the two states of (9A-7) are nonsensical; even though there is no mathematical prohibition against such states, they don’t pertain to any relevant physical situation.