Principles and Concepts
of Quantum Mechanics
of Quantum Mechanics
Implications of
Quantum Mechanics
Quantum Mechanics
16. Probability and Constraints on Interpretations
of Quantum Mechanics.
Summary
The probability law of quantum mechanics is defined and explained. It provides severe limits on interpretations.
Suppose we consider basic quantum mechanics, QMA, as an interpretation. It is assumed in QMA that (1) only the wave functions, which obey linear Schrödinger equations, exist (no particles or hidden variables); (2) there is no collapse of the wave function; (3) there are no ‘sentient beings’ outside the laws of quantum mechanics; and (4) there is no a priori assumption of a probability law.
The states. To see the implications of these assumptions, suppose we do an experiment—perhaps a Stern-Gerlach experiment—on an atomic system that has n possible states. Before the measurement, the system has state
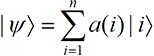
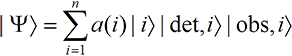
QMA properly implies classical perception. To see if this multiple-versions-of-you scenario gives a reasonable interpretation, under the assumption that our current perceptions correspond to those of one of the versions of the observer, we first need to check whether the perceptions of each version violate any of our experiential perceptual rules. From the section on Classical Perception, we see that each version perceives a single version of reality; that two observers never disagree; and that successive measurements are consistent. And, anticipating the results from No Evidence for Particles, we see that each version will perceive a universe that appears to be made of classical, localized particles. So the many-worlds, QMA-based interpretation, strange as it seems with its many versions of each of us, appears to do an excellent job.
Problems with the probability law. There is, however, one major problem with the QMA scheme—the |a(i)|2 Probability Law of principle [P10]. This law cannot hold within QMA. We will give a (relatively) simple form of the argument here, with supplementary arguments in Details of Probability.
We work from Eq. (16-2). First, the only entities that perceive in QMA are the versions of the observer, so all statements about perception must refer to the perceptions of the versions of the observer. Second, one might conjecture that only one version of the observer is ‘aware.’ But one can show (see Details) that all versions are equally aware.
Now each version,
The consequence is thatFurther, one version must be singled out—see Details of Probability—as the one corresponding to my perceptions.
[P17] The probability law cannot hold in the bare QMA scheme, where all versions of the observer are perceptually equivalent on each run.
[P18] The probability law implies there must be some mechanism, not within QMA, which singles out one version of the observer as the one corresponding to my perceptions.In addition, we argue in Details that
[P19] One does not obtain a satisfactory interpretive scheme by simply adding the probability law as a postulate to the first three principles of QMA because the singling out mechanism required by [P17] is not specified.
Principles [P17], [P18] and [P19] provide significant constraints on interpretations.

