Principles and Concepts
of Quantum Mechanics
of Quantum Mechanics
Implications of
Quantum Mechanics
Quantum Mechanics
9A. Details of Classical Consistency of Perception.
Summary
Quantum mechanics prohibits perception of more than one classical version of reality, and it implies two observers can never disagree on what they perceive.
We wish to indicate here that quantum mechanics does not conflict with our perception of a seemingly classical world. The main ideas used are that only versions of the observer perceive (Schrödinger’s Cat, principle [P2]) and that the versions of reality, including the versions of the observers, are in isolated, non-communicating universes (Separate Universes in Quantum Mechanics).
To illustrate the principles, we consider an experiment on an atomic system with K states,
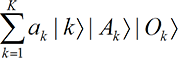
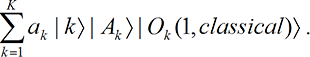
[P6] Basic quantum mechanics prohibits perception of more than one version of reality.
Observers must agree. Next we consider principle [P7], on the agreement of observers. We ask two observers to write down their perceptions and then ask the second observer to look at the first observer’s result and write “agree” or “disagree.” Because the interactions are local and separable, a cause in the past can never produce a classically inconsistent effect in the future within a version. This general principle implies that the state vector is
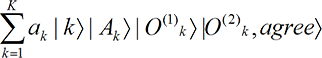
[P7] Quantum mechanics implies that two observers can never disagree on what they perceive.
Successive observations are consistent. We now consider principle [P8]. We start from state (9A-1) and have the observer look twice at the dial. Then we have state
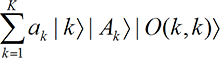
[P8] If two observations of a single result are made successively, quantum mechanics implies the same consistency of results as one obtains in a classical universe.
The same argument would apply if one did multiple experiments; results are always consistent within a version, and versions of the observer cannot ‘see’ from one isolated universe to another.
Finally, we consider principle [P8], in the technical case, on the consistency of successive measurements. As an example, we might have a spin
To actually write out the states to show this is a notational nightmare, so we will talk it through. We suppose there is a device, M, that splits the beam of incoming particles into N different trajectories, and on each trajectory, there is a readout, R, that says no (no detection) or yes (detection). Then on each of the N possible trajectories, we put a similar device, M plus a similar readout. We designate the state of the apparatus before the experiment by a 0 subscript. Then for any of the N+1 sets of apparatus, we have
and hence for the special case
Now we do the compound experiment. After the first apparatus, there will be N versions of reality. In version k, there will be the particle state,
If one measures the same property twice in a row, quantum mechanics implies one will get the same result.
In summary, the perceptions of ‘the observer’ in quantum mechanics will never disagree with what is expected classically. (So the only problem with quantum mechanics is that we don’t know which version of reality will pop up.)
Measurement Theory The principles of Quantum Mechanics and Classical Perception constitute much of the content of what is called measurement theory. Only in measurement theory, they are taken as axioms, needed to make sense of measurements in quantum mechanics, rather than as principles deduced from quantum mechanics itself. These derived principles show that in all circumstances, quantum mechanics itself implies a ‘classical’ consistency of perceptual results—‘measurements’—even though no classical (that is, single-version-of-reality, effect-follows-from-cause) reality was assumed.
We note that, there is a principle on the perception of eigenvalues, which should have been derived before principle [P8]. It is derived as principle [P8A] in section 14B.
Superselection rule. Preferred basis problem. The principles of Quantum Mechanics and Classical Perception also imply it is appropriate to apply a superselection rule to the various versions of reality. Linear combinations of, say, the various states of the observer are not prohibited, but (as in the case where one has one universe with charge 2e and another with charge 3e) when there is no interaction between different solutions of the Schrödinger equation, nothing—no new physical insight—is gained by considering linear combinations of the states.
Thus the preferred basis problem, in which linear combinations of versions of the observer are considered, seems to be a red herring (see also the derivation of principle [P6] and Measurement Theory). No version of the observer will ever perceive anything besides a single version of reality.
More specifically, if the versions of the observer write down what they perceive, no version of the observer will ever write down that she perceives anything other than a single (classical) version of reality, no matter what basis one uses. Suppose, for example that we have two final states, 1 and 2. Then one might try a basis where ‘the observer’ has states
But there is still no term where the observer writes down that she perceives both states 1 and 2. And the two parts of

